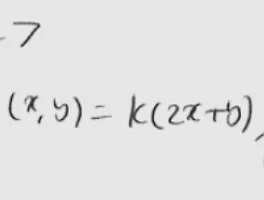Check
- E[X|Y] = ?


- 위 example을 풀 수 있는가?
- X와 Y의 covariance의 정의는?
- X와 Y의 covariance를 E[XY] - ____ 의 꼴로 나타내면?
- Covariance가 0이라는 것은 어떤 의미인가?
- Covariance가 0이면 X와 Y는 independent 한가?
- X와 Y가 independent 하다면 covariance는 0인가?
- Correlation coefficient의 정의는?
- Correlation coefficient의 범위와 의미는?
- Correlation coefficient의 분모의 의미는?
- y=ax+b로 표현될 때 X와 Y의 covariance는?
- Cauchy schwarz inequality는?(a,b,c,x,y,z에 대해)
- Cauchy schwarz inequality를 vector로 확장하면? 성립하는 이유는?
- Correlation coefficient의 절대값이 1보다 작음을 증명할 수 있는가?

조건부 평균과 조건부 분산의 개념


Example은 다시 풀어보자.

Covariance의 정의

Covariance의 의미, independence와의 관계

Independent는 uncorrelated에 포함되는 개념이다.

Correlation coefficient의 정의와 의미

y=ax+b에서 correlation coefficient가 -1 혹은 1이 되는 것을 증명

Correlation coefficient가 -1~1사이임을 코시 슈바르츠 부등식으로 증명한다. Hilbert space의 개념을 이용해서 함수간의 내적을 생각할 수 있고, 여기서도 코시 슈바르츠 부등식이 만족함을 이용하여 증명할 것이다.

'수업 정리(개인용) > 확률 및 통계(한양대 이상화교수님)' 카테고리의 다른 글
| 확률 및 통계(한양대 이상화교수님) lec14 : 확률변수의 변환 함수 (0) | 2021.02.12 |
|---|---|
| 확률 및 통계(한양대 이상화교수님) lec13 : 상관계수와 연합정규분포 (0) | 2021.02.09 |
| 확률 및 통계(한양대 이상화교수님) lec11 : 연합확률밀도함수와 조건부확률밀도함수 (0) | 2021.02.03 |
| 확률 및 통계(한양대 이상화교수님) lec10 : 다중변수 및 연합분포 (0) | 2021.02.01 |
| 확률 및 통계(한양대 이상화교수님) lec9 : 정규분포 (0) | 2021.02.01 |