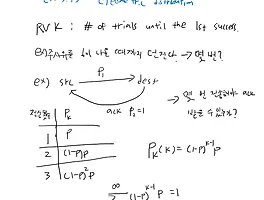
Check
- Discrete RV는 무한할 수 있는가? 그에 mapping 되는 event들은 discrete 해야 하는가?
- Continuous일 때는 어떤가?
- Continuous RV에서 P(X=x)가 정의 되는가? 안된다면 대안은?
- Pdf의 정의는? cdf와의 관계식은?
- Pdf의 함수값은 1보다 클 수 있는가?
- Uniform distribution이란? 가정되는 예시는?
- Analog에서 digital로의 변환 과정은? Uniform distribution이 언제 가정되는가?

Event는 continuous 해도 그와 mapping 되는 RV가 discrete 하다면 discrete이다(discrete이면 discrete이라는 당연한 이야기이다). RV는 finite하거나 countably infinite할 수 있다.

Discrete RV에서는 cdf보다는 pmf를 많이 사용한다.

Continuous RV와 그에 mapping되는 event는 둘 다 uncountably infinite 하다. 이 경우에는 한 점에서의 확률이 정의가 되지 않는다. 우리는 0이라고 생각하기로 한다.
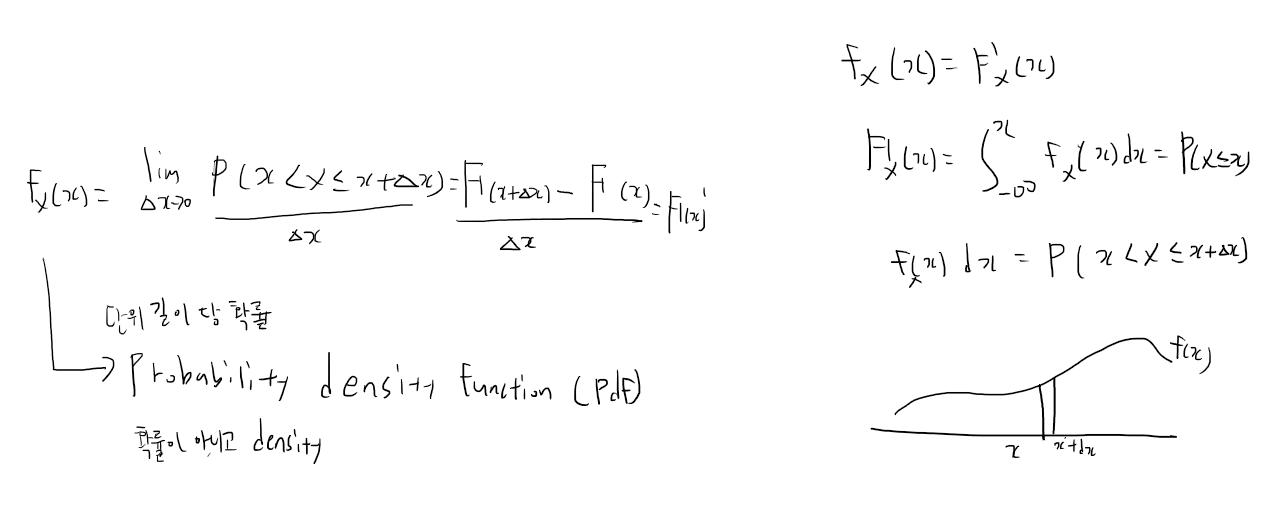
그래서 위와 같이 pdf를 정의하여 사용한다. 정의하고 보니 cdf의 도함수임을 알 수 있다. 공간 당 산소 분자의 개수와 같이 측정할 수 없는 것들은 density로 표현한다. 여기서도 점 당 확률이 정의되지 않으니 density로 나타낸다.

조건이라고 하셨는데 성질인지 조건인지 헷갈린다.




양궁에서 과녁의 특정 구역을 맞출 확률을 구할 때, 원의 넓이를 사용한다. 별 생각 없이 이렇게 풀어왔지만, 이것은 내재적으로 uniform distribution을 정의한 풀이이다.

신호 처리 관련해서 재미있는 얘기를 해주셨다. 아날로그 신호가 sampling과 quantization으로 digital 신호가 되는데, 여기서 발생하는 quantization error의 분포가 uniform distribution이라고 가정된 채로 많이 사용된다.
'수업 정리(개인용) > 확률 및 통계(한양대 이상화교수님)' 카테고리의 다른 글
| 확률 및 통계(한양대 이상화교수님) lec6 : 조건부 평균 (0) | 2021.01.12 |
|---|---|
| 확률 및 통계(한양대 이상화교수님) lec5 : 확률변수의 평균과 분산 (0) | 2021.01.11 |
| 확률 및 통계(한양대 이상화교수님) lec3 : 확률 변수의 정의 (0) | 2021.01.02 |
| 확률 및 통계(한양대 이상화교수님) lec2 : 독립사건과 확률 (0) | 2020.12.29 |
| 확률 및 통계(한양대 이상화교수님) lec1 : 조건부확률과 Bayes 정리 (0) | 2020.12.26 |