
지난 knn 과제처럼 CIFAR-10을 사용한다.
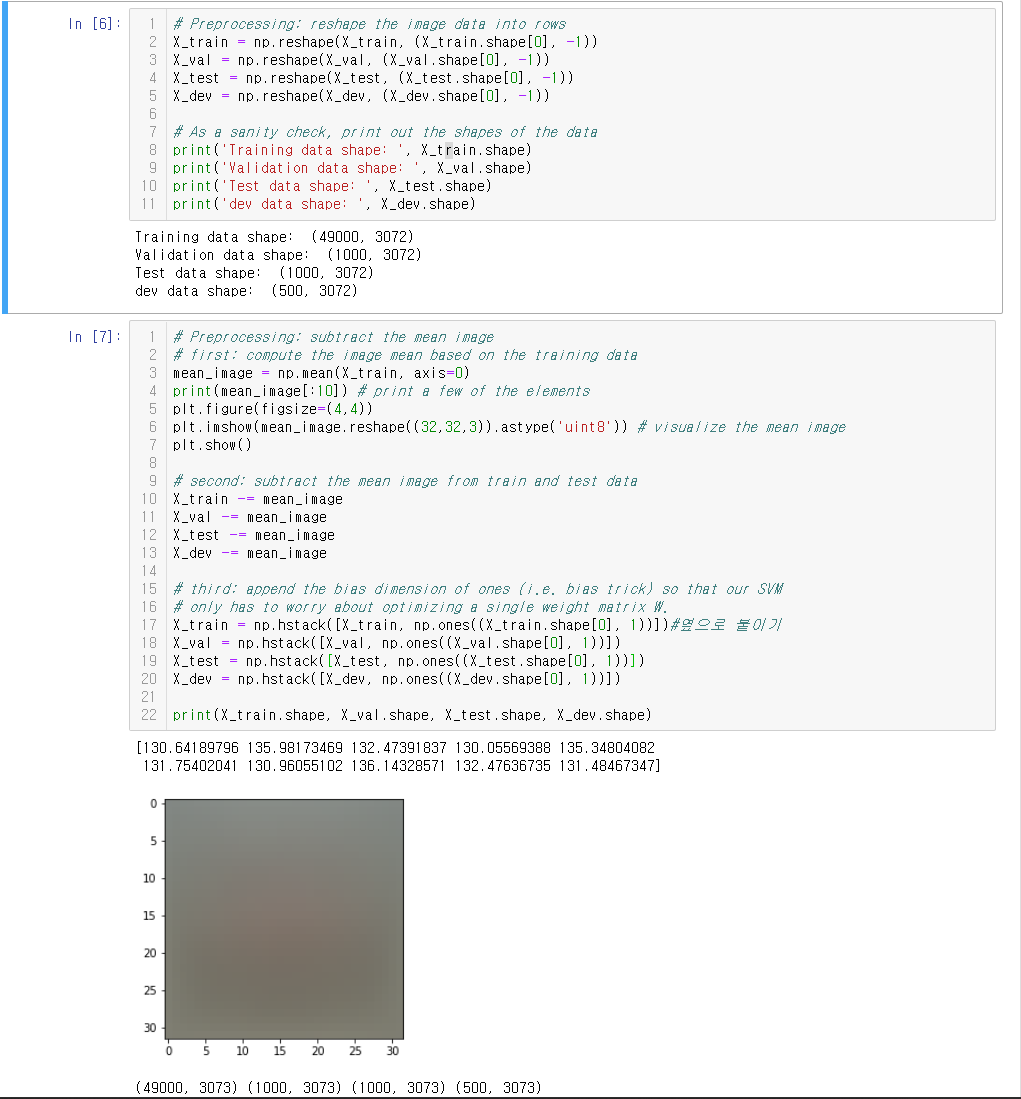
데이터를 나누고 reshape하고 전처리 하는 과정이다. Per pixel mean을 구해 mean image를 구하고 데이터에게 뺄셈한다. Bias를 사용하지 않기 위해 X의 가장 오른쪽 열에 1을 붙여주고 weight의 shape[0]도 한 칸 늘려준다(bias trick).

linear_svm.py를 열고 svm_loss_naive를 구현해야 한다.

이중 for문 안에서 우리는 score의 각 원소에 접근할 수 있다. Score[j]는 j번째 class에 해당한다. j==y[i]라면 정답 class인 것이므로 loss에 더해줄 필요가 없으므로 continue 한다. 또한 margin이 0 이하라면 더하지 않는다(hinge loss의 그래프를 떠올리면 쉽다). 그 이하는 gradient를 구하는 부분이다. dLoss/dScore[j]는 loss가 num_train으로 나누어지므로 1/num_train이다. dLoss/dCorrect_score는 마찬가지이나 -1의 계수가 붙어있으므로 -1/num_train 이다. 이후로는 chain rule을 이용해서 구하면 된다. 재미있는 점은, 정답 class에 해당하지 않는 W의 gradient가 X[i]/num_train이고, 정답 class에 해당하는 W의 gradient에 -X[i]/num_train이가 더해진다는 점이다. Gradient를 적용할 때 W에서 빼므로, 가령 고양이 이미지가 들어오면 고양이에 해당하는 W에는 고양이의 상수 배 만큼 더해지고, 고양이에 해당하지 않는 W에서는 고양이의 상수 배 만큼 빼지게 된다. 이것은 나중에 다시 다루도록 하겠다.

Numerical gradient와 비교하여 실수는 없었는지 확인한다.

Inline Q1. Numerical gradient와 analytic gradient간에 차이가 발생하는 이유는 무엇일까? 물론 컴퓨터의 소수점 계산의 정밀도에 한계가 있는 것도 맞다. 하지만 위의 결과의 빨간 밑줄 친 부분을 보면 다른 경우에 비해 유독 차이가 크다. Hinge loss는 margin이 0인 지점에서 미분이 불가능하다. 애초에 gradient가 정의되지 않는 점이므로 임의로 정하는 수 밖에 없다. 내가 구현한 코드를 보면 margin이 0보다 클 때만 loss에 더해주고 0보다 작거나 같을 때에는 더해주지 않는다. dMargin/dScore를 구한다고 하자. Score = 2, correct_score = 3이라고 하면 margin = 2-3+1 = 0이다. 그러므로 if문 안에 들어가지 못하기 때문에 gradient를 더해주지 않는다(0이다). 이제 Numerical gradient를 구해보자. h=0.001로 가정하면 gradient는 (0.001-0)/0.001 = 1이 된다.
이런 일이 발생하는 빈도를 줄이려면 미분 불가능한 hinge 부분을 멀리 보내서 최대한 안 만나는 수 밖에 없다. 그러려면 safety margin을 1이 아니라 더 큰 수를 줘서 실질적으로 correct_score가 상당히 커지지 않는 한 hinge를 만날 수 없게 하면 된다.
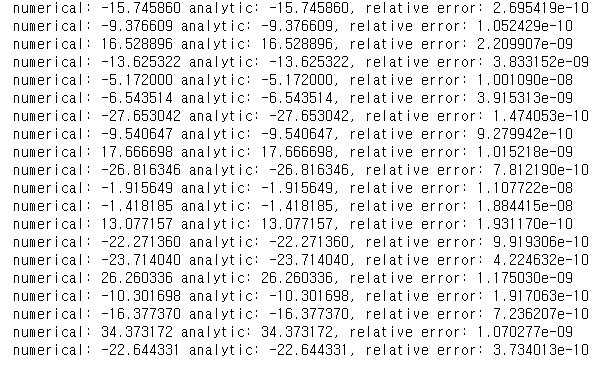
Safe margin을 100으로 늘린 이후의 결과이다. Numerical gradient와의 차이가 줄어들었다.

Loop 없이 loss와 gradient를 구하는 함수이다. Gradient를 구하는 부분을 설명하자면,

이런 식으로 생긴 computational graph를 떠올리면 된다. Margin의 local gradient를 어떻게 구할 수 있을까? Margin에 적용되는 masking 연산이라는 것은 1. 정답 class에 해당하는 margin을 0으로 만들고 2. 0보다 작은 값을 0으로 바꾸는 것이다. 그렇기 때문에 zeros로 초기화 한 후 margin값이 0 이상인 위치에만 1의 gradient를 부여한다. 그 후 1/N(num_train)과 곱한다.
Correct_score의 경우 한 원소가 score의 한 행의 모든 원소에게 broadcast되어 뺄셈 연산을 한다. 하지만 masking 연산을 고려한다면 실제로는 margin의 0보다 큰 원소에만 빼진 셈이다. 그렇기 때문에 margin>0을 axis 1 방향으로 sum 한 후 -1을 곱하게 된다(뺄셈 연산이므로). 그 후 num_train으로 나누면 된다.
Score의 특정 원소들을 가지고 만든 게 correct_score이므로 그 원소들의 위치를 찾아 correct_score의 gradient를 더해준다. 그리고 score의 gradient를 이용해 W의 gradient를 구할 수 있다.

Gradient를 구할 수 있으니 이제 linear_classifier.py로 들어가서 SGD를 구현하면 된다. Batch를 구성하고 loss와 gradient를 구한 후 W에 gradient와 learning_rate의 곱을 빼주면 된다.
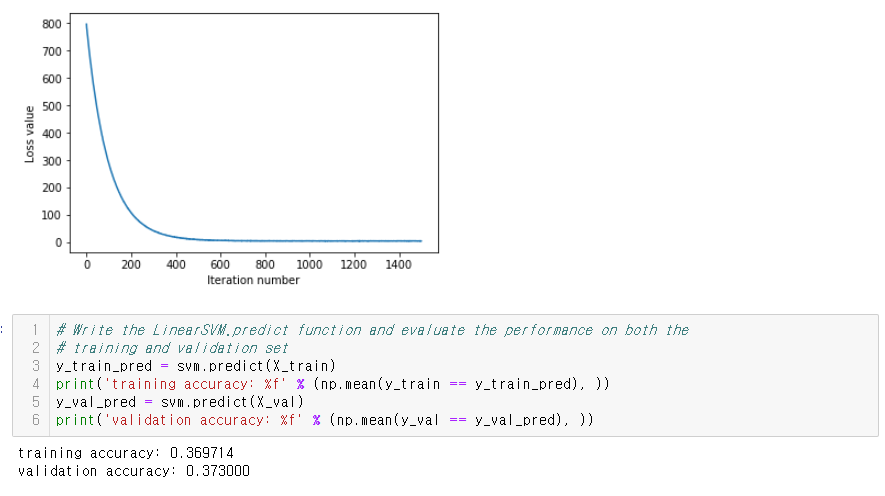
결과는 이렇다.

Validation set을 이용해서 총 4개의 조합의 hyperparameter를 실험해 볼 것이다.

lr이 1e-7이고 reg이 2.5e4일때 결과가 좋았다. Val accuracy가 0.382로 튜닝하기 전보다 0.009 올라갔음을 알 수 있다. Hyperparameter를 어떻게 정하느냐에 따라 아예 학습이 되지 않을 수도 있다.

Test 시에는 결과가 validation 때보다 떨어졌다.

W를 시각화 한 것이다. 각 class에 해당하는 W가 그 class의 템플릿의 형상을 보이고 있다. 왜 이런가에 대해서는 Lecture 2 review에서 언급한 적이 있다.


위에서 한번 언급한 gradient를 loop을 돌며 구하는 코드이다. 보면, W의 j번째 열, 즉 정답 class와 관련이 없는 W에는 X[i]의 상수 배가 뺄셈 되고, 정답 class에 해당하는 W에는 X[i]의 상수 배가 덧셈 된다. 이런 과정을 반복하다 보면 W는 해당하는 label이 붙은 X의 모습을 닮아갈 것이다.
'수업 정리(개인용) > cs231n' 카테고리의 다른 글
| CS231N Spring 2020 Assignment1 : Softmax (0) | 2020.09.26 |
|---|---|
| CS231n 2017 Lecture 5 : Convolutional Neural Networks (0) | 2020.09.25 |
| CS231n 2017 Lecture 4 : Introduction to Neural Networks (0) | 2020.09.19 |
| CS231n 2017 Lecture 3 : Loss Functions and Optimization (0) | 2020.09.12 |
| CS231n 2017 Lecture 2 : Image Classification (0) | 2020.09.12 |



