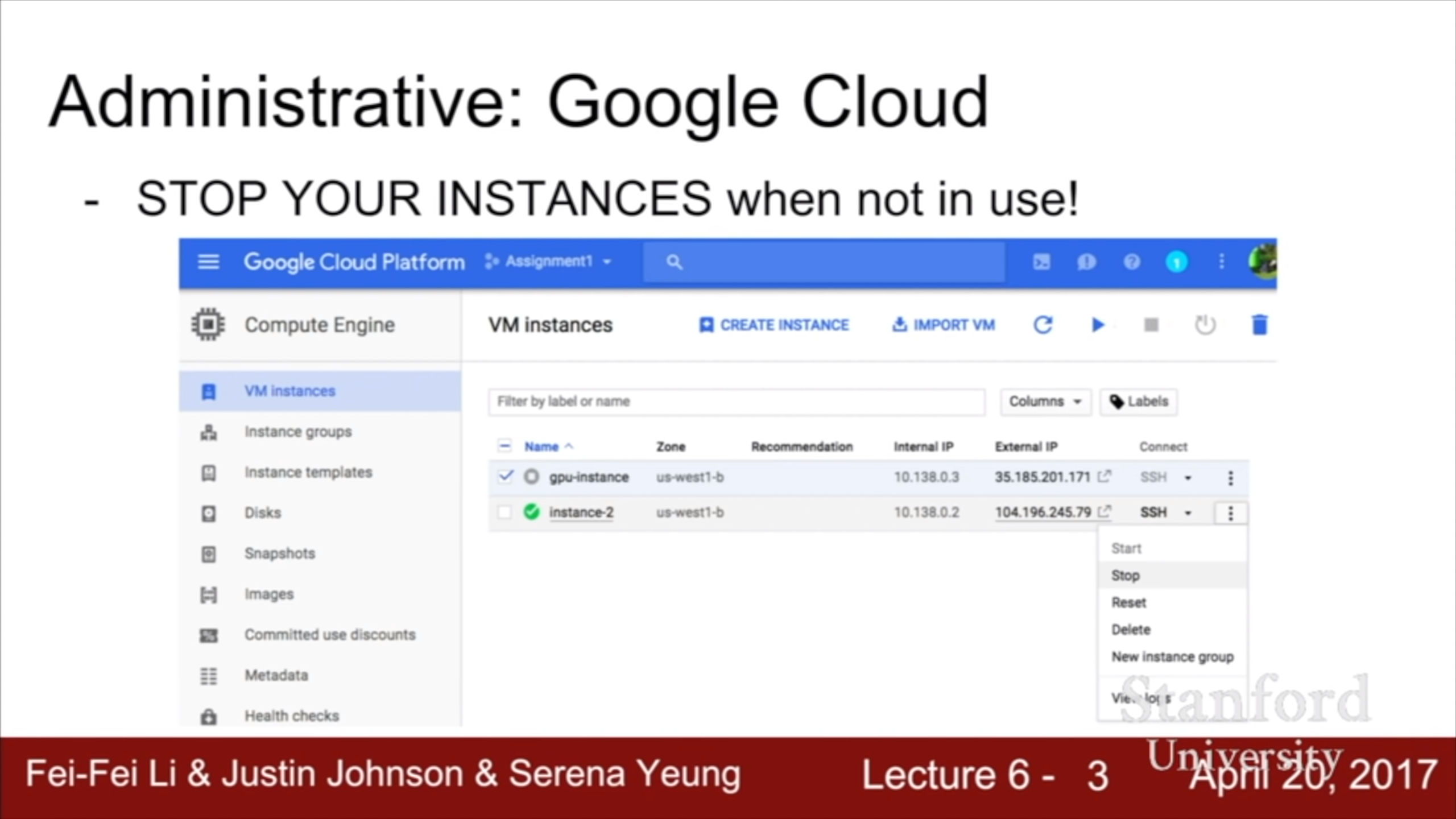

오랜만에 본다.
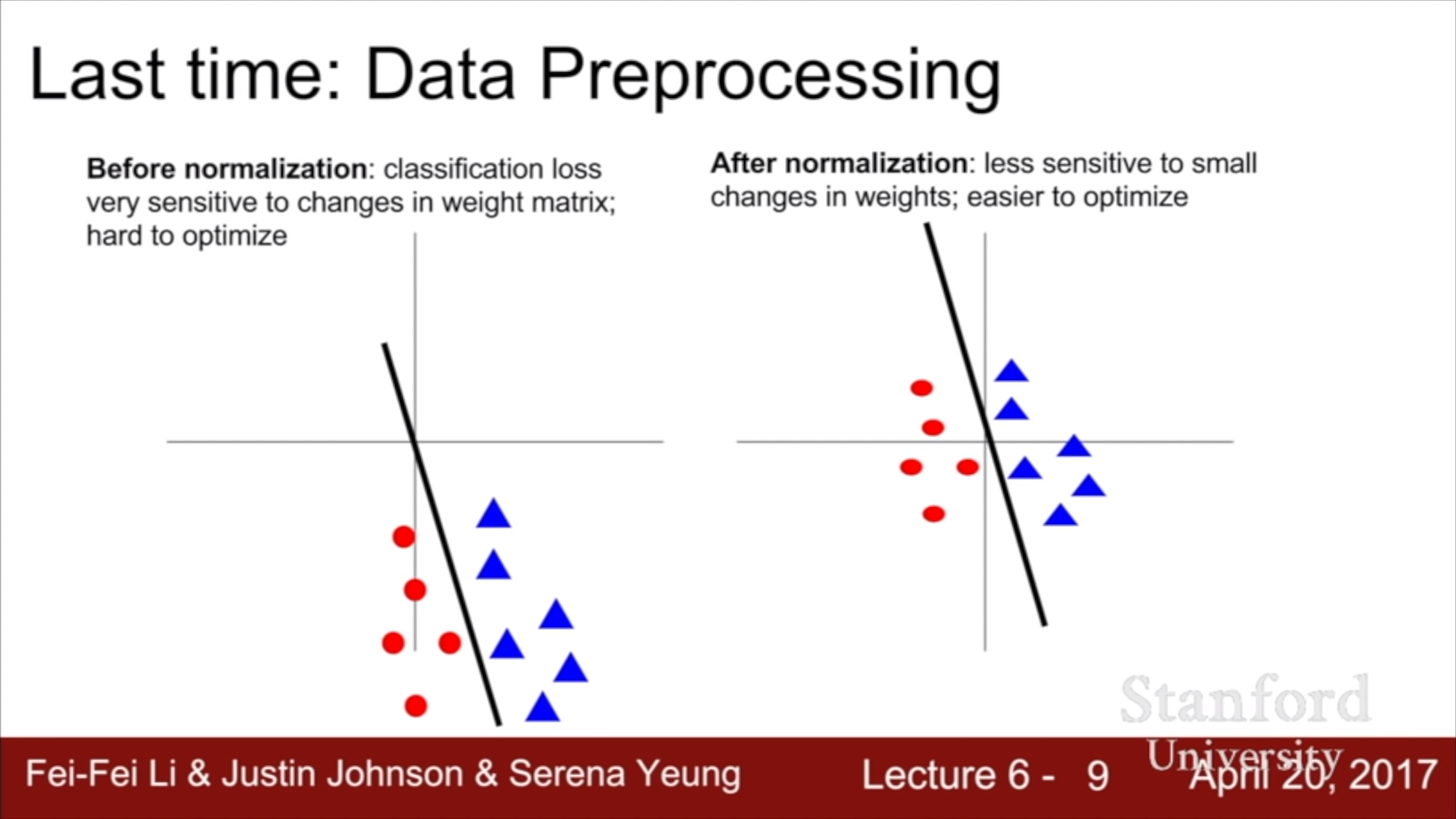
저번 강의에서 다룬 normalization에 대한 첨언이다. 같은 classifier라도 data의 value가 크면, weight가 약간만 바뀌어도 classification 결과가 바뀔 수 있다. Normalization을 통해 model을 좀 덜 sensitive 하게 만들 수 있다.

오늘 배울 것들

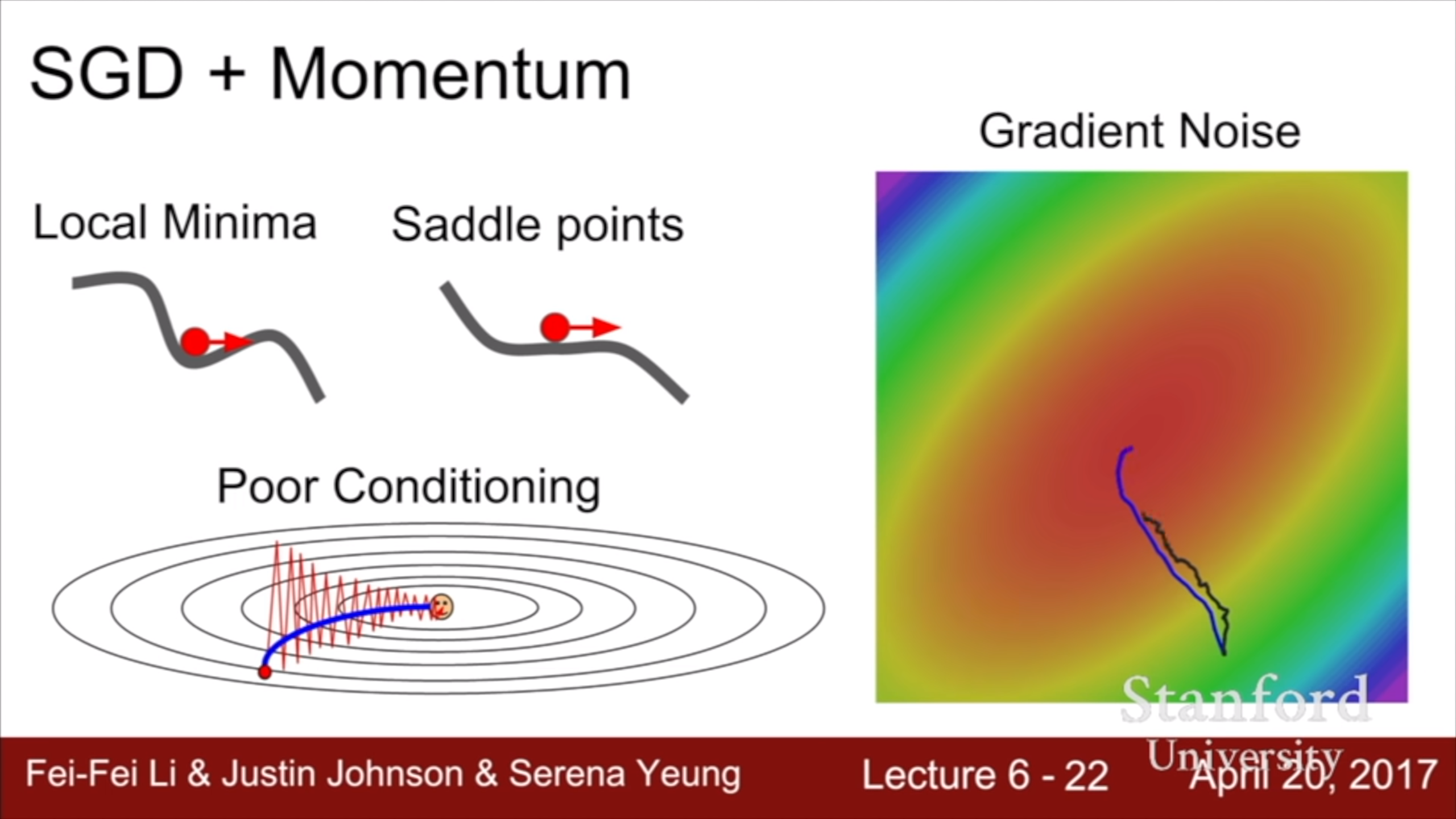
SGD의 단점1 : Gradient에만 의존하기 때문에 상대적으로 완만한 방향으로는 진전이 느리고 경사가 급한 방향으로 많이 이동해서 지그재그로 경사면을 내려간다. 위 그림을 가로 축 w1, 세로 축 w2라고 생각하면, w1의 gradient가 w2의 gradient에 비해 많이 낮다. 이럴 때 condition number가 높다고 한다. 차원이 늘어나면 가장 낮은 gradient와 가장 큰 gradient의 비율 차이가 더 커지는 경향이 있다. 그 많은 gradient 값 중에서 가장 작은 값과 가장 큰 값의 차이는 상당할 것이다. 고차원 벡터를 다루는 deep learning에서 이건 심각한 문제다.

SGD의 단점2 : local minima나 saddle point에 도달하면 멈춰버린다. Saddle point 주변에서 매우 느려진다.
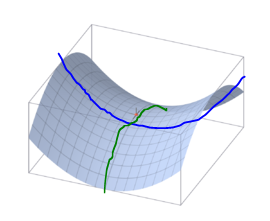
Saddle point란 이렇게 어느 직선에서는 그 점이 최대값이고, 어느 직선에서는 그 점이 최소값인 지점을 말한다. 고차원 함수에서는 local minima보다 더 문제가 되는데, 차원이 높을 수록 그 모든 방향으로 loss가 증가할 확률이 적기 때문이다. Saddle point는 어느 방향으로는 loss가 줄고, 어느 방향으로는 loss가 느는 지점이므로 상대적으로 더 흔하다.
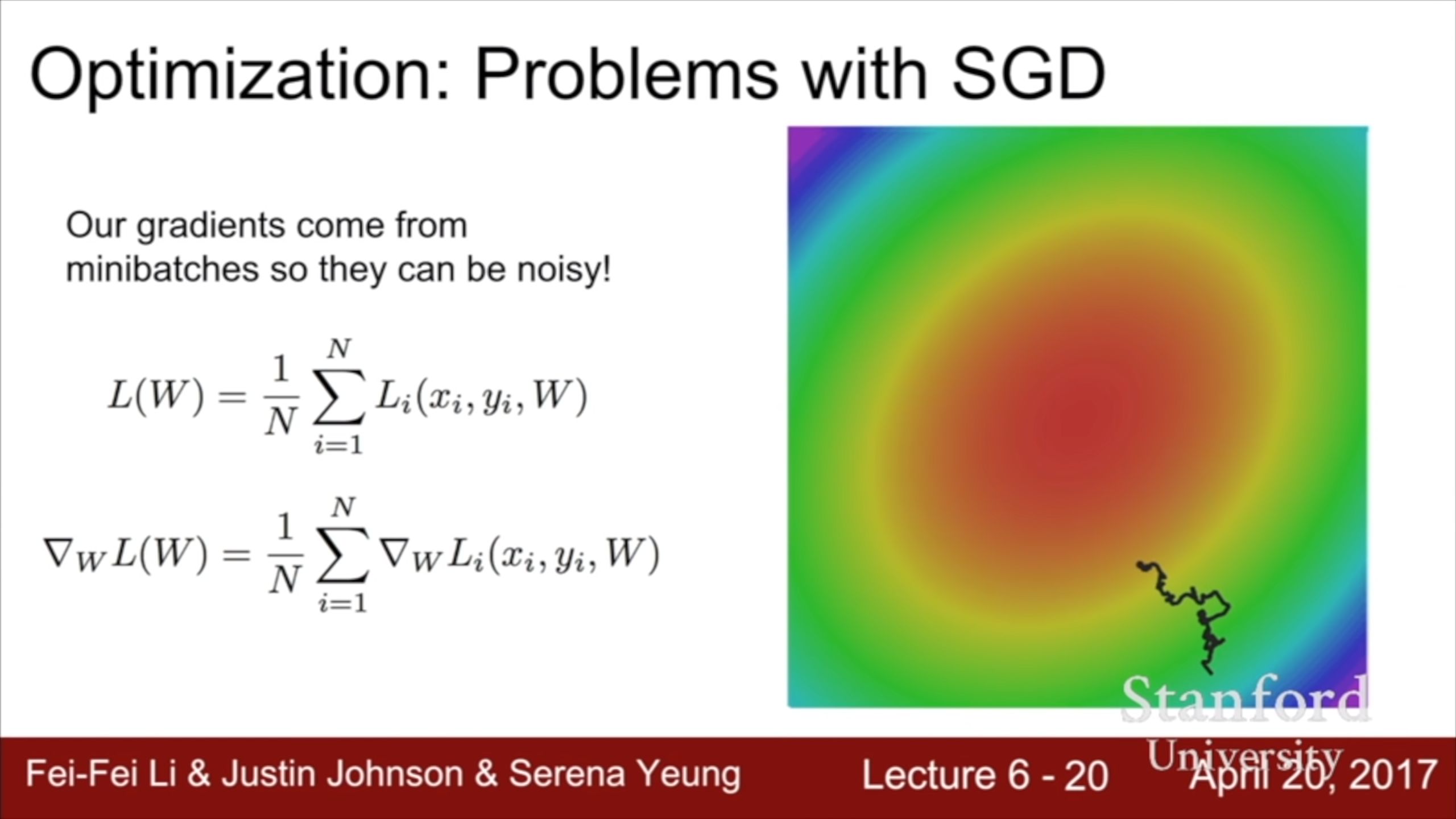
SGD의 단점3 : Stochastic 이기 때문에 noisy하다.

현재 gradient 뿐 아니라 이전의 gradient 정보도 사용한다는 것이다. 관성의 법칙을 떠올리면 쉽다.
이제 관성이 생겼기 때문에 gradient가 낮은 방향으로도 빠르게 갈 수 있다. 단점 1 해결
Local minima나 saddle을 만나 gradient가 0이 돼도, 이전 step들의 gradient를 decay해서 갖고 있기 때문에 통과할 수 있다. 단점 2 해결
Gradient를 계속 더해 나가다 보니 noise도 누적돼서 어느정도 average에 가까워지게 된다. 단점 3 해결
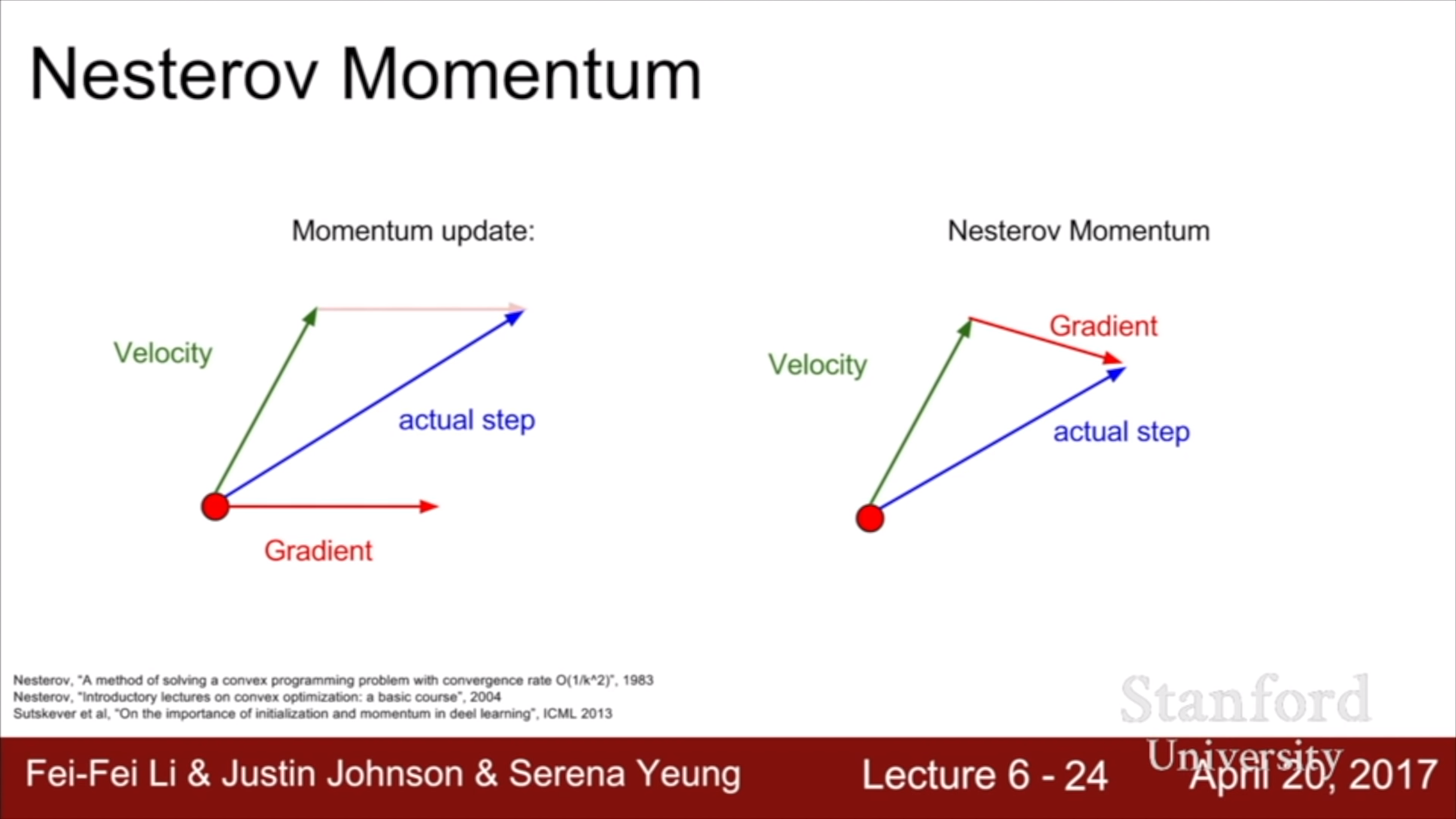
Nesterov Momentum은 처음 들어보는데, 흥미롭다. Velocity를 구하는 부분은 momentum이랑 같고, 그 velocity만큼 이동했다고 치고 그 시점에서의 gradient를 구한다. 그리고 그 gradient가 가리키는 지점으로 이동한다. 마치 내가 A 고객센터에 전화를 걸건데, 거기서 B 고객센터로 연결해준다는 사실을 미리 알 수 있다면 애초부터 B 고객센터에 거는 게 효율적일 것이다. 재미있는 알고리즘이다.

수식으로 나타내면 위와 같다. 우리가 늘 쓰던 방식대로 바꾸기 위해 x를 치환한다. 치환해보니 현재의 velocity와 과거의 velocity와의 차이를 구해 보정하는 의미가 담겨있는 걸 알 수 있다. 치환해서 정리하는 식은 아래와 같다.
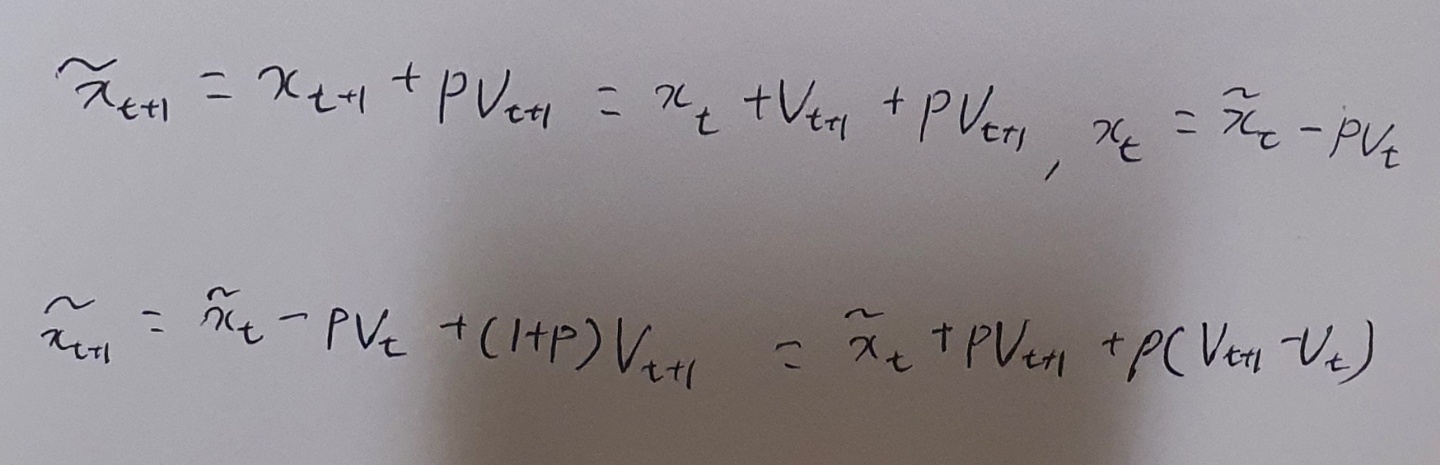
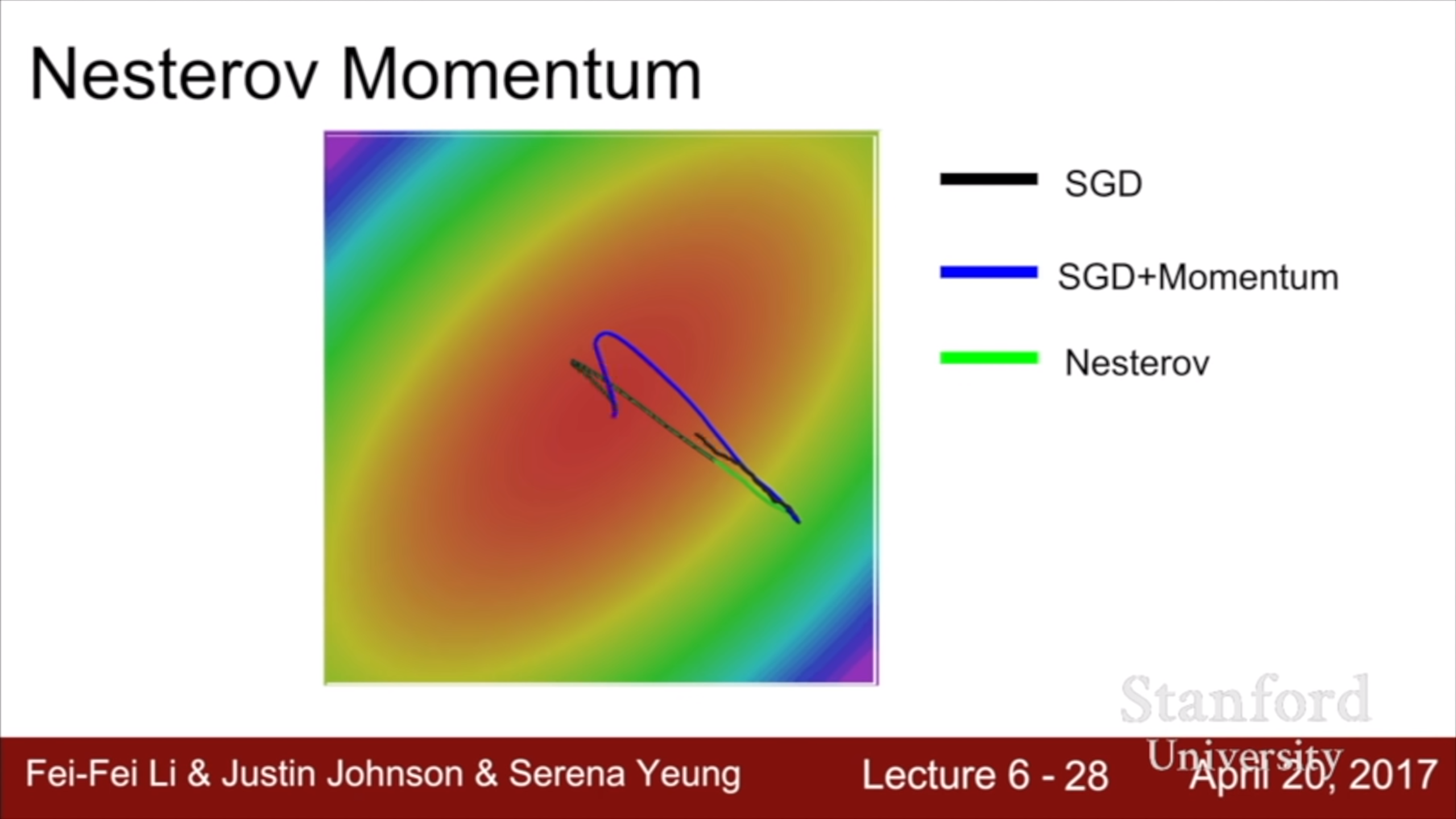
Nesterov 방식이 minima를 지나쳤을 때 빠르게 보정되어 돌아오는 것을 볼 수 있다.
이런 momentum 기법들을 사용하면 좁고 깊은 minima에는 수렴하지 못하는 것 아니냐는 질문이 들어온다. 그런 sharp한 minima들은 사실 bad minima이고, overfitting이 일어나는 곳이므로 피하는게 낫다고 한다.
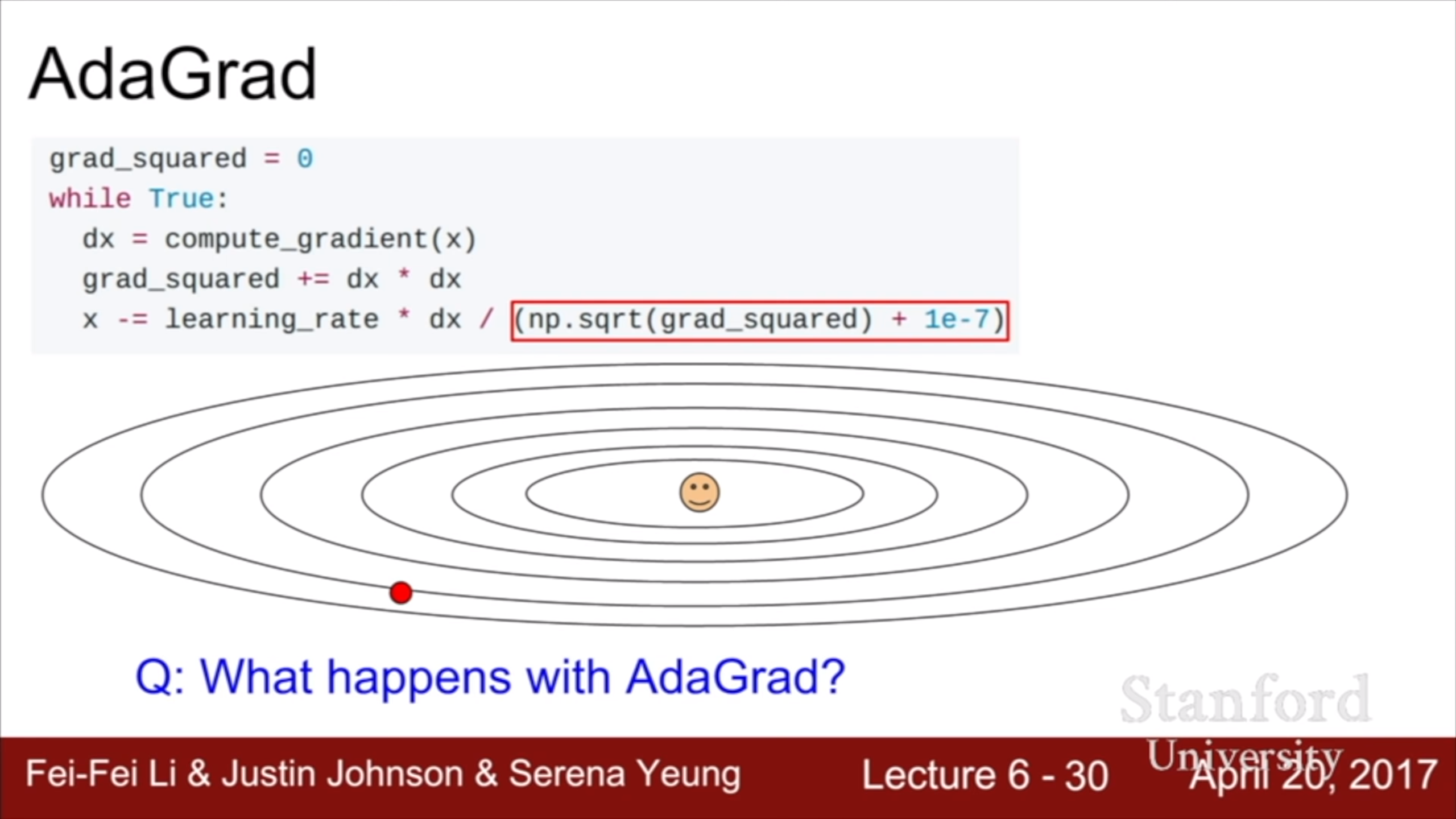
AdaGrad에서는 gradient의 제곱을 계속 더해서 update시에 나누어준다. Gradient가 큰 방향으로 덜 가게 규제하는 효과가 있어서 지그재그 현상을 줄일 수 있다. 하지만 분모가 계속 누적되어 커지기 때문에 step이 쌓일 수록 이동 거리가 점점 작아진다. Non convex function에서 saddle에 걸릴 수도 있다.
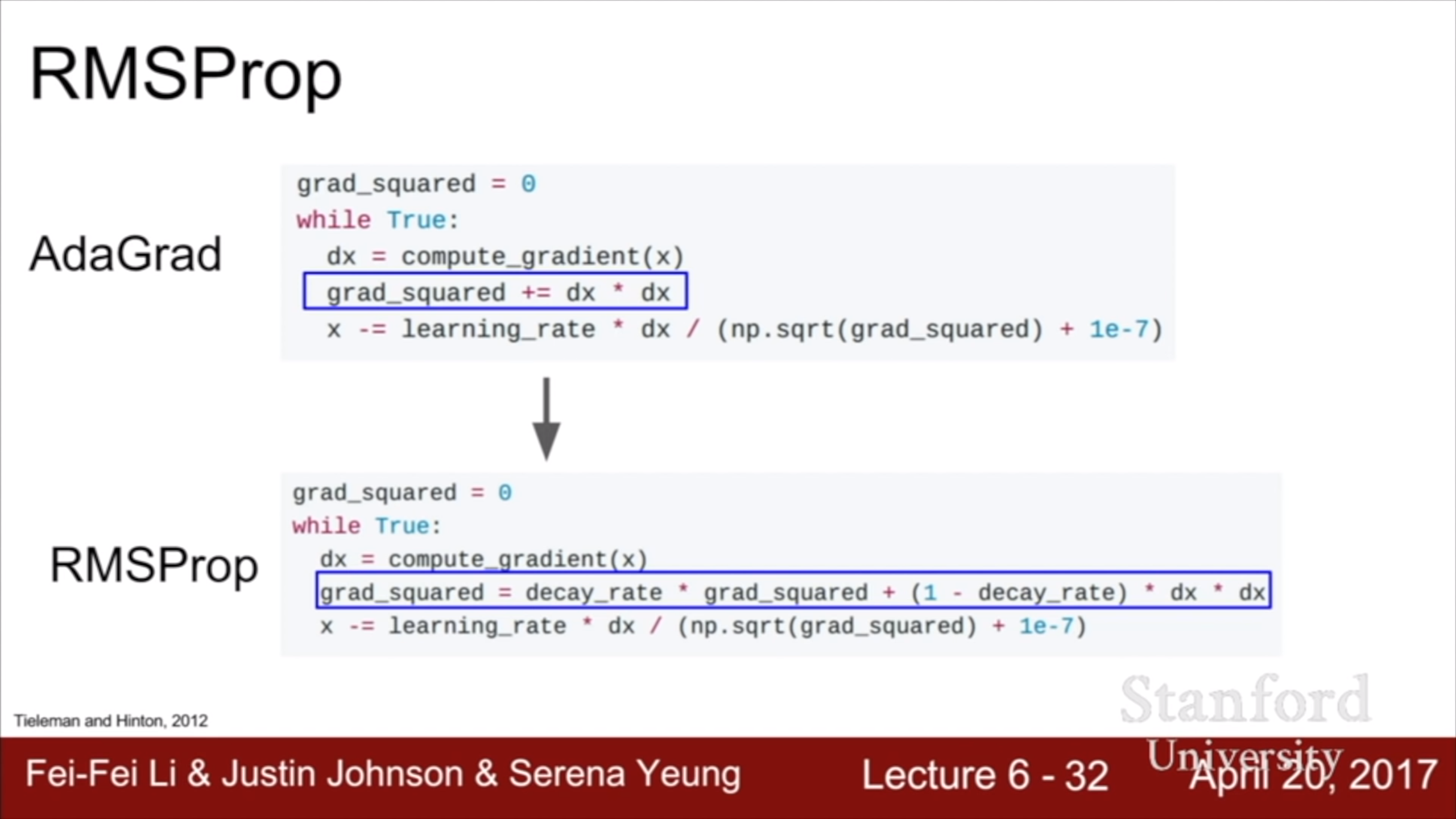
RMSProp이 그걸 해결해준다. 전체적으로 AdaGrad와 비슷한데, gradient의 제곱을 더할 때 decay를 걸어서 이동 거리가 덜 줄어들도록 하는 것이다.

Momentum과 AdaGrad / RMSProp을 합친게 adam이다.
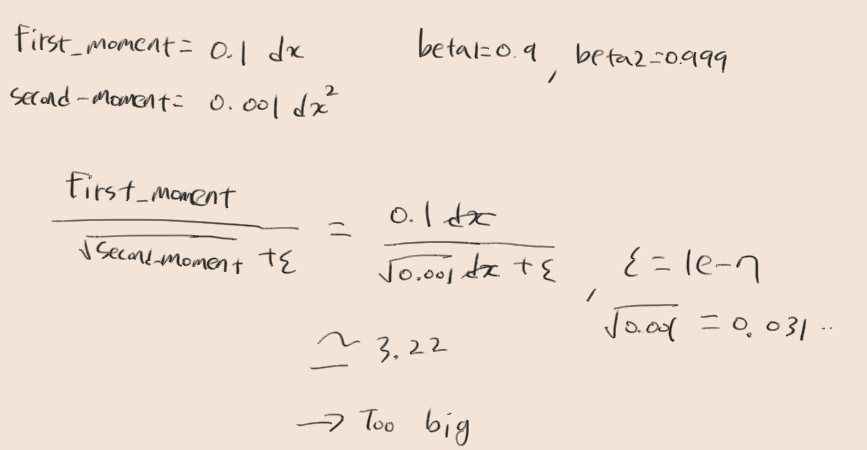
beta2는 beat1보다 큰 값으로 설정하는 것이 original paper의 권고이다. 그럴 경우 초반의 step size가 너무 커지게 된다.

그걸 방지하기 위해 bias correction이 들어갔다.
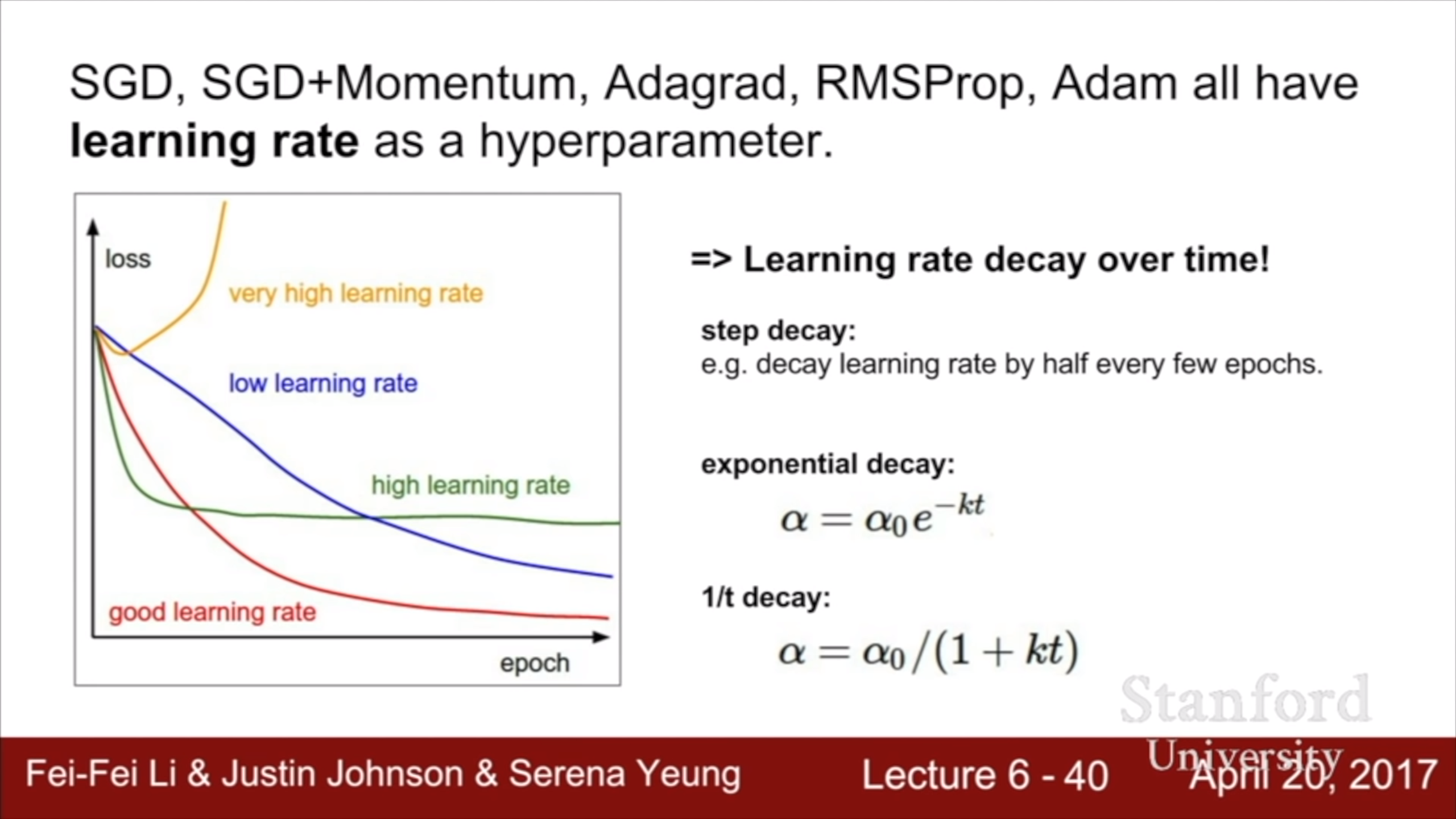
Learning rate decay의 다양한 방법들. Adam에서는 보통 decay를 잘 쓰지 않는다.
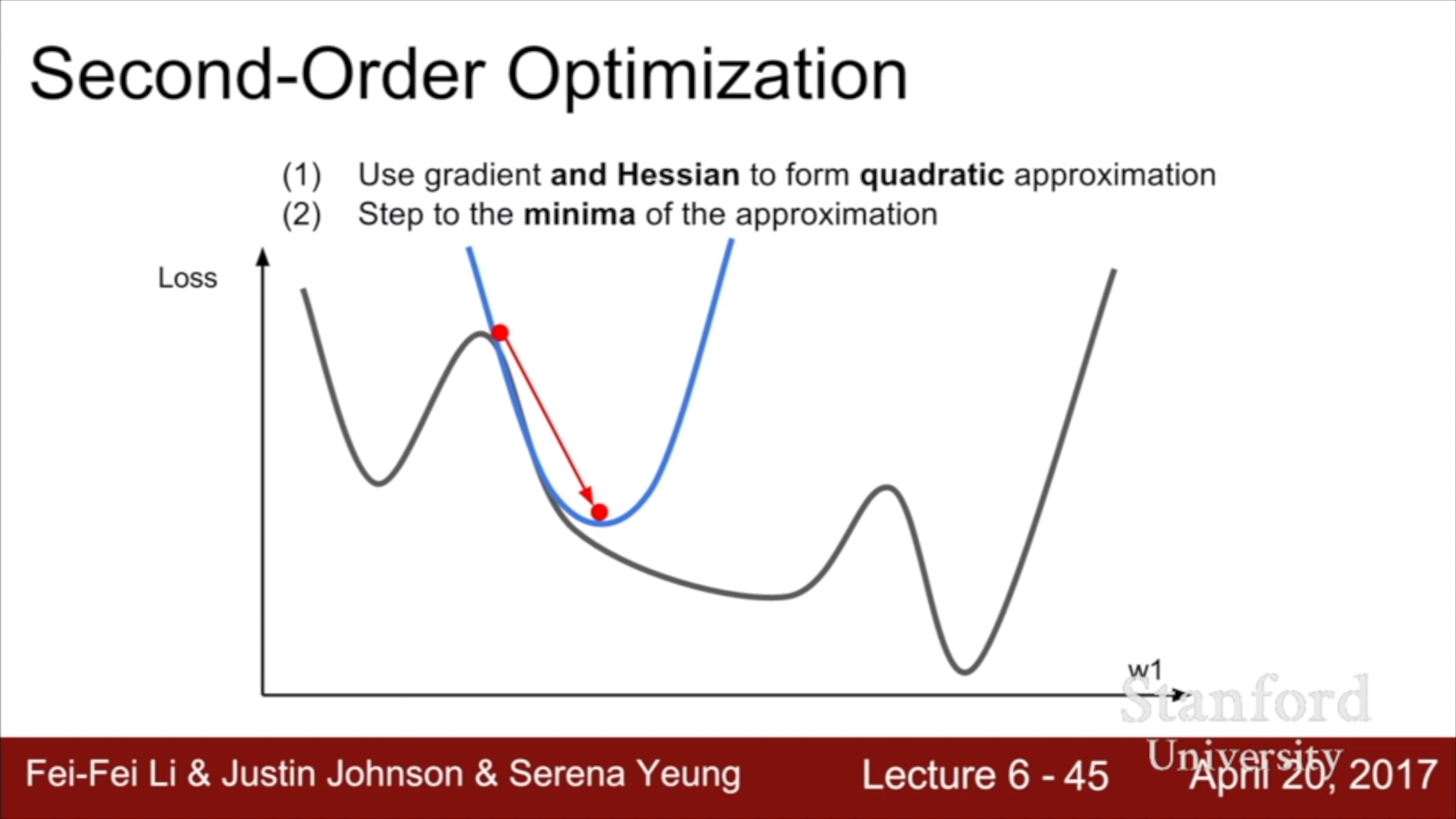

테일러 정리를 이용한 2차 근사로서의 뉴턴 방법을 이용해서 optimize하는 방법이 있는데, 계산 비용이 너무 많이 들어서 실제로 사용하긴 어렵고, 위의 두 방법은 그것의 근사 버전이다.
L-BFGS는 stochastic에 취약하기 때문에 mini batch를 활용하기 어렵고, non convex일 때 성능이 좋지 않다. 그래도 style transfer 같은 분야에서 쓰이기도 한다. 웬만하면 adam을 쓰자.
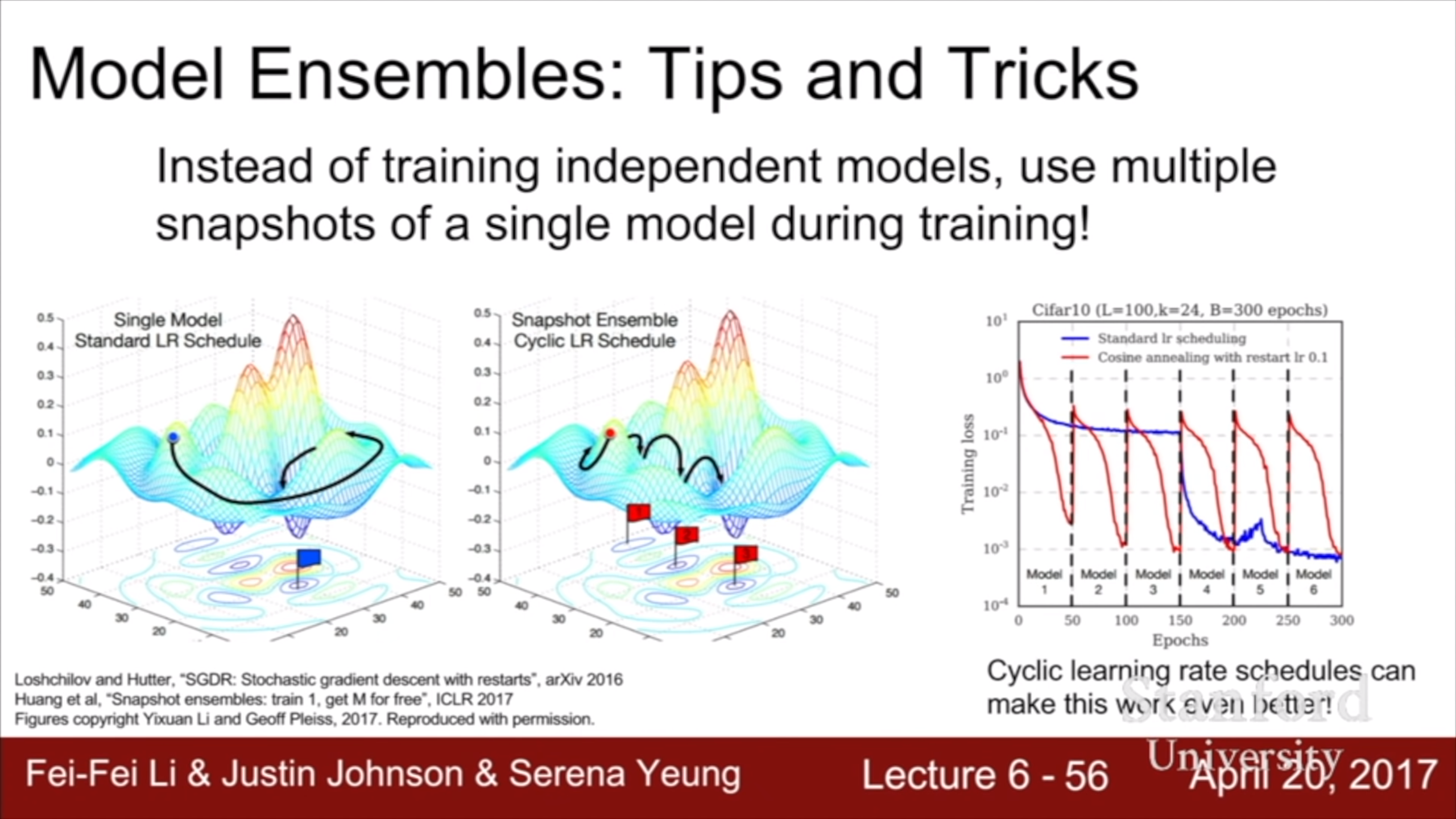
흔히 알고있는 앙상블과 달리 이건 하나의 모델을 여러 시점에서 기억해 놓고 각각을 앙상블 하는 방법이다. 오른쪽 사진을 보면 learning rate을 시점별로 스케줄링 해서 각 시점마다 서로 다른 곳으로 converge 하게 만든다. 한 번의 train으로 앙상블을 할 수 있다.

Train 시에 weight 값들을 decay하면서 누적시키고(momentum 때 처럼) 그 값을 test 시에 사용하는 방법도 있다.

Dropout이 잘 되는 이유는 모델이 상대적으로 적은 feature만 가지고 판단하게 해서 일반화 성능을 올려주기 때문이다.
다른 해석으로, dropout을 앙상블로 볼 수 있다. 원래 뉴런에서 임의의 절반을 꺼버린 서브 모델로 훈련을 하는건데, 이 서브 모델 각각을 개별적인 모델로 보면 앙상블이다. 하지만 N개의 뉴런이 있다면 2^N개의 가능한 서브 모델이 있다. 앙상블을 하려면 그 모든 모델들의 output을 더해서 평균을 내야 하는데, 어떻게 할까?

그걸 수식으로 나타내면 저런 적분 식이 된다.

우측 하단의 수식을 보면, dropout probability를 0.5로 줬을 때 output의 기대값이 보인다. Test 할 때의 output에 0.5를 곱한 값이다. 즉 test output에 dropout probability를 곱하면 모든 서브 모델들의 output의 평균이 된다.

Regularization의 common pattern을 보면, 모델 train 할 때 약간의 random성을 부여해서 혼란을 줘서 overfit을 못하게 하는 것이다. Dropout이 그런 방법 중 하나지만 batch norm도 저번 강의에서 말했듯이 regularization 효과가 있다.

Augmentation 역시 overfitting을 막아주는 효과가 있다.
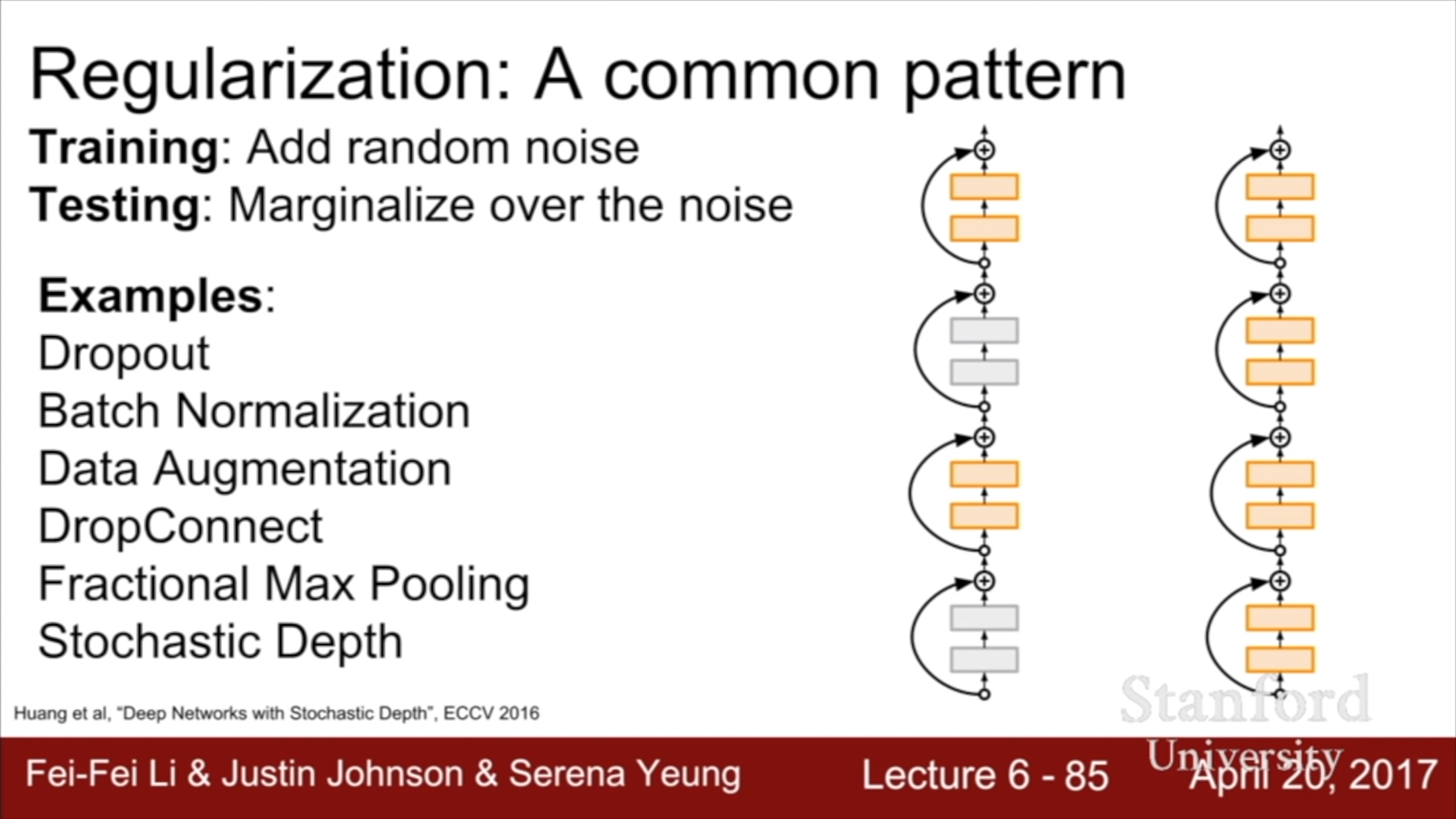
이렇게 많은 방법들이 있다. 실전에서는 batch norm이면 거의 해결이 되고, 안되면 dropout 정도를 추가하는 식이라고 한다.
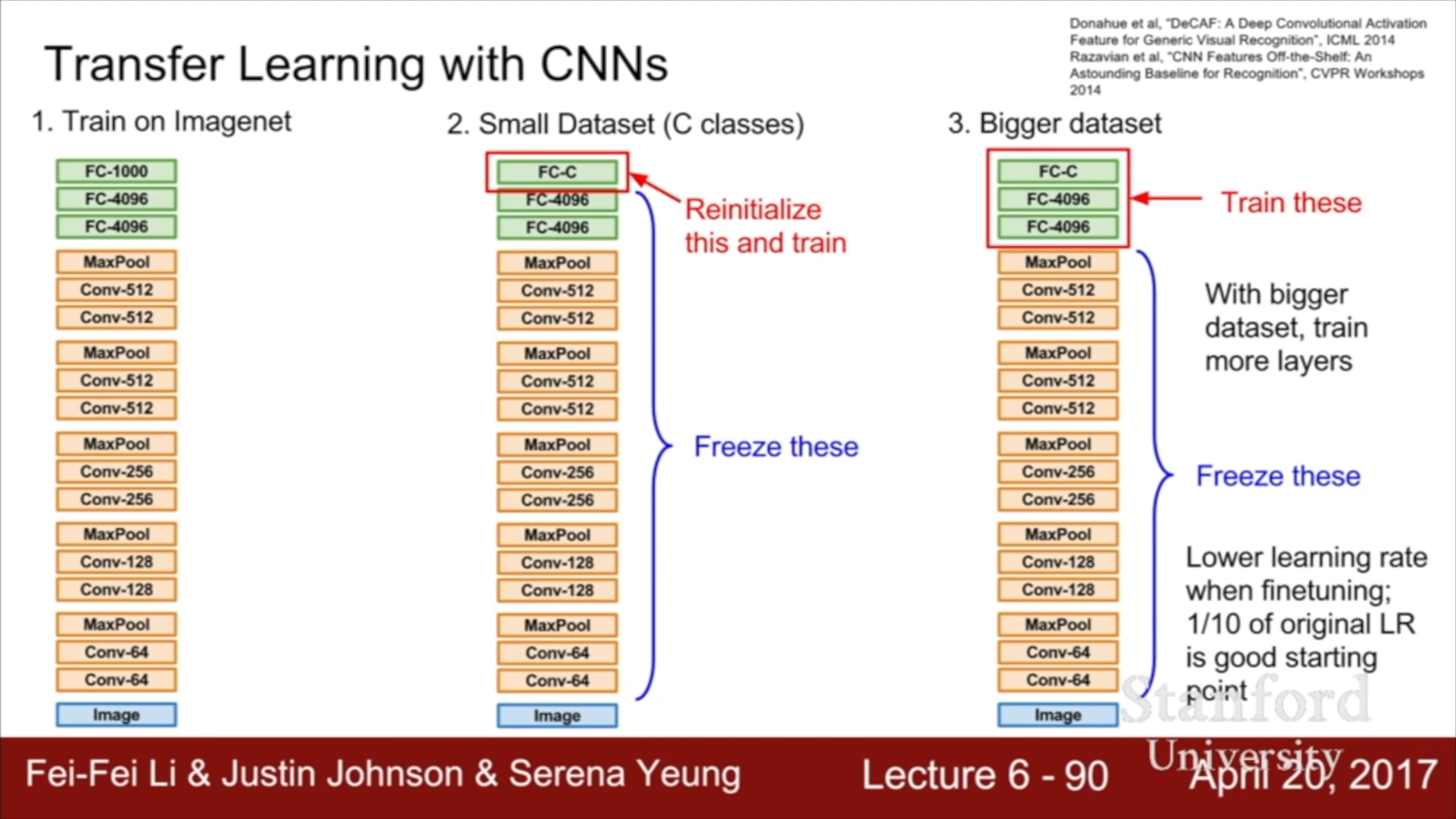
Overfitting을 막으려고 regularization을 했지만, 현실에서는 data가 부족해서 overfit이 많이 난다. 전이 학습은 pre-
training/fine-tuning 방식을 뜻한다. 이미 훈련된 모델을 가져와서 내 domain의 적은 data로 fine-tuning 하는 것이다. 얼마전 리뷰한 R-CNN(yun905.tistory.com/13?category=876803)도 ImageNet에서 pre-train된 AlexNet을 가져와 object detection에서 fine-tune 하여 사용하였다. CNN의 경우, 내 domain에 사용하려면 우선 top layer를 새 것으로 바꾸고 학습을 시키는 것은 필수다. 그 후 여력이 된다면 나머지 layer들도 학습시킨다. Fine tuning 시에 learning rate를 pre train의 0.1배 정도로 해서 pre training된 모델을 너무 망치지 않도록 한다.
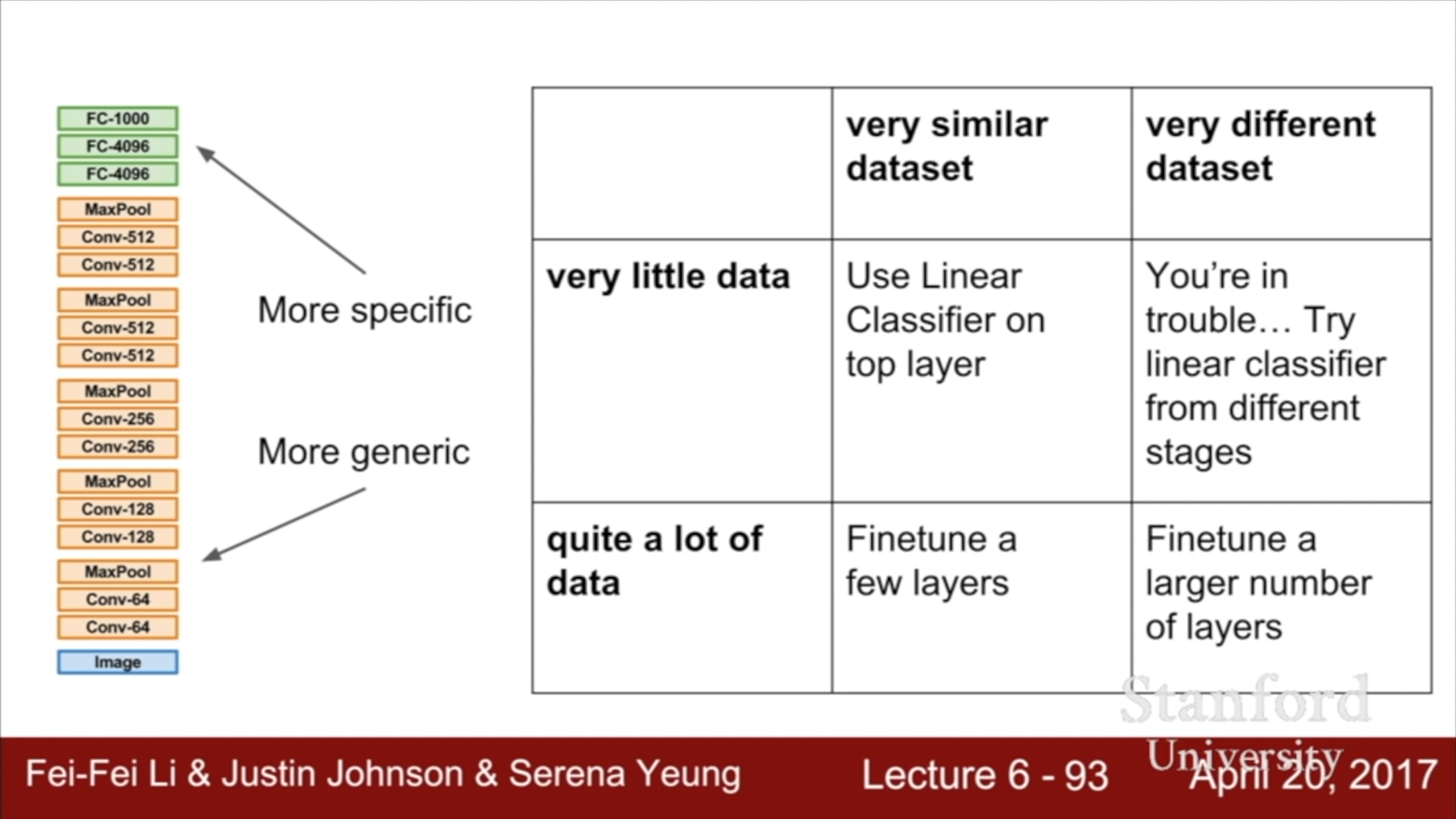
사용하고자 하는 domain이 pre-train된 모델과 다를 경우 문제가 된다. 가령 ImageNet에서 학습된 VGG를 엑스레이 사진 인식에 사용하려면 잘 안될 가능성이 높다. 엑스레이 사진이 많으면 fine tuning을 많이 시켜서 쓰면 되는데, 적을 때가 문제다. CNN의 낮은 계층에서는 낮은 level의 feature를 뽑고(oriented edge, color 등등) 높은 계층에서 그 feature들을 활용해서 더 추상적이고 domain specific한 feature를 뽑으니, 조금 낮은 계층에서 얻은 feature(즉 좀 더 일반적인 feature)를 사용해서 해보는 것도 방법이다.
Computer vision에서 전이 학습은 거의 표준이므로 거의 사용하는 방향으로 가는게 좋다. 흥미로운 dataset을 찾았는데 크기가 백 만개 이하라면 전이 학습을 고려하자.
'수업 정리(개인용) > cs231n' 카테고리의 다른 글
| CS231n Lecture 9 : CNN Architectures (0) | 2020.12.26 |
|---|---|
| CS231n 2017 Lecture 8 : Deep Learning Software (0) | 2020.12.26 |
| CS231n 2017 Lecture 6 : Training Neural Networks I (0) | 2020.10.03 |
| CS231N Spring 2020 Assignment1 : Features (0) | 2020.10.01 |
| CS231N Spring 2020 Assignment1 : Two Layer Net (0) | 2020.09.27 |



