레드 블랙 트리

기존의 이진 검색 트리는 깊이가 원소 수 만큼 늘어날 수 있기 때문에 성능을 보장 받지 못한다는 단점이 있다. 그래서 이진 검색 트리에 몇 가지 제약을 걸어서 만든 것이 레드 블랙 트리이다.

레드 블랙 트리의 조건

1. 루트는 블랙

2. 리프는 블랙

3. 노드가 레드이면 자식은 블랙(no double red)

4. 루트에서 리프까지 만나는 블랙의 수가 일정하다.

+ 삽입된 노드는 레드

여기서 모든 리프가 블랙이라는 것은 우리가 생각하는 리프에 해당하는 말이 아니다.

위와 같이 자식이 하나이거나 없는 경우 NIL이라는 가상의 리프 노드를 붙여주고 블랙으로 만든다.

레드 블랙 트리는 이진 검색 트리에 이런 저런 조건을 건 것이므로 기본적으로 이진 검색 트리라고 할 수 있다. 즉 모든 삽입과 삭제는 이진 검색 트리의 방식대로 하고, 조건이 깨졌을 때 그것을 회복하는 알고리즘을 돌린다고 이해하면 된다.

레드 블랙 트리의 삽입

삽입될 자리를 찾아가는 것은 이진 검색 트리와 동일하다. 삽입된 노드는 레드이므로, 부모가 블랙인 경우 아무 문제도 없다. 문제는 부모가 레드일 경우에 발생한다.

부모인 p가 레드라면 p의 부모 p^2는 블랙일 수 밖에 없다. x의 형제 노드도 블랙일 수 밖에 없다. s의 색에 따라 두 가지 경우로 나눌 수 있다. 참고로 여기서는 p가 p^2의 왼쪽 자식일 경우를 설명하고 있다. 오른쪽 자식일 경우 정확히 대칭된 방법으로 하면 된다.

s가 블랙인 경우 : restructure

1. x가 p의 오른쪽 자식인 경우, p를 기준으로 왼쪽으로 회전 후 2로 이동

2. x가 p의 왼쪽 자식일 경우, p^2 기준으로 오른쪽으로 회전, p와 p^2 색 교환

우리가 double red를 해결할 수 있는 경우는 그림1 같은 경우다. x가 p의 오른쪽 자식일 경우는 해결할 수가 없다. 그런 경우에는 p를 기준으로 왼쪽으로 회전 시켜서 그림1과 같은 경우로 만들어줘야 한다.

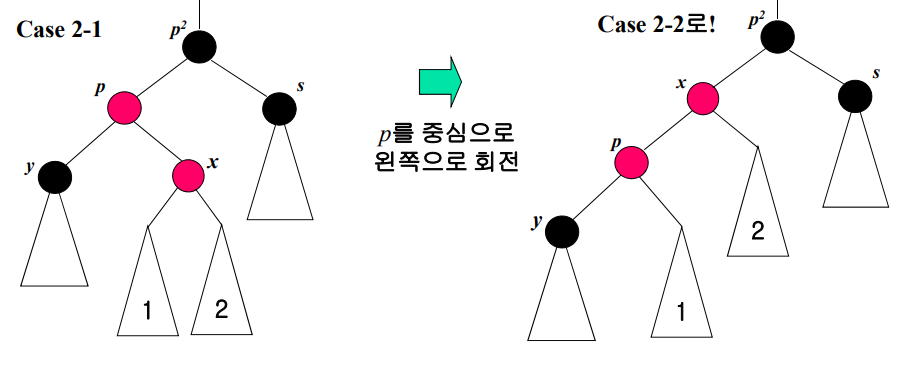
1과 같은 상황에서 회전을 마치고 나니 p^2을 기준으로 왼쪽 방향으로 double red가 발생해서 2와 같은 상황이 되었다. 이제 우리가 해결할 수 있는 문제이다.

p^2를 기준으로 오른쪽으로 회전 시킨후 p와 p^2의 색을 교환 하였다.

s가 레드인 경우 : recolor

Restructure가 어려운 편이었고 recolor는 쉽다.

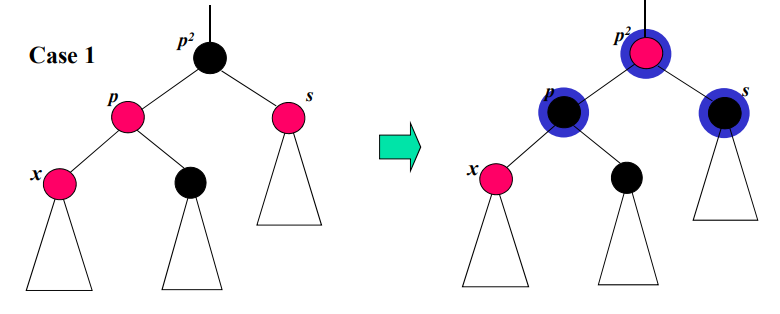
p^2와 p,s의 색을 교환하면 끝이다. 다만 p^2가 갑자기 레드가 되어 버렸으므로 동일한 문제가 발생할 수 있다. 재귀적으로 해결하면 된다.

레드 블랙 트리의 삭제

자식이 없는 노드를 삭제하는 것은 그냥 날리면 끝이다. 자식이 두개 있는 경우, 이진 검색 트리와 똑같이 삭제 노드에 직후 원소를 넣은 후, 해당 직후 원소가 원래 있던 곳에 가서 삭제를 재귀 호출하면 된다. 물론 그 직후 원소는 왼쪽 자식이 없을 것이다. 즉, 자식이 두 개인 노드를 지우는 문제도 결국 자식 하나인 노드를 지우는 문제를 재귀 호출하게 된다.

따라서 자식이 하나일 경우에 대해 생각해보자.

삭제하고자 하는 노드가 x이고 x의 유일한 자식 c가 있다고 하자. x가 레드이고 c가 블랙인 경우 단순히 p와 c를 연결하면 끝이다. x가 블랙이고 c가 레드인 경우, p와 c를 연결한 후 c를 블랙으로 칠해주면 된다. 문제는 둘 다 블랙일 경우이다.