CS231n 2017 Lecture 6 : Training Neural Networks I

이번 강의의 overview이다.

다양한 non-linear function에 대해 알아볼 것이다.

Sigmoid는 위와 같이 생겼다. 3가지 문제점이 있는데,
1. 중심에서 멀어지면 gradient가 죽는다.
2. Output이 0~1이므로 zero-centered 되어 있지 않다.
3. exp() 함수가 비용이 크다.
1,3은 직관적으로 이해가 가는 부분이다. 그런데 zero-centered는 왜 문제가 되는걸까?

저기서 w1,w2,...wn의 local gradient가 x1,x2...xn이다. 그런데 x가 이전 layer의 sigmoid를 거쳐서 나온 값이라고 하면 x는 모두 양수이다. L = w1x1 + w2x2 ... 라고 하자. Chain rule을 적용할 때 L의 gradient와 w의 local gradient를 곱한 것이 w의 gradient 이다. 그런데 w1~wn의 local gradient가 다 양수이므로 w1~wn의 gradient는 L의 gradient의 부호를 따라가게 된다. 즉 w1~wn의 gradient의 부호가 모두 동일하다는 것이다. 이것을 2차원으로 축소시켜서 그래프로 나타낸 것이 위의 슬라이드 이다. 저기서 가로 축을 w1, 세로 축을 w2라 하면, 1 사분면 방향이나 3 사분면 방향으로 밖에 이동할 수가 없다. 그래서 저런 지그재그 path가 나오게 된다.
이것은 뉴럴넷의 input이 zero-centered 되어야 하는 이유이므로, 당연히 input data에도 똑같이 적용된다.

Sigmoid의 zero-centered 문제를 해결한 tanh 함수이다. 하지만 gradient가 죽는 문제는 해결하지 못했다.

그래도 sigmoid보다 낫긴 하다.

Relu. x>0일 때 한정으로 gradient가 죽는 문제가 없다. 당연히 수렴도 빠르다. 엄청 자주 쓰이는 함수이다. 하지만 zero-centered 문제가 있고, x<0일 때 gradient가 죽는다.

그래서 발생하는 문제가 dead relu이다. 간단히 말해, 내 data manifold에서 어떤 값을 넣어도 0보다 작은 output이 나오는 weight를 가지고 있으면, 절대로 update 시킬 수 없다. 예를 들어 bias가 -10000이면 input에 상관 없이 0보다 작은 output이 나올 것이다. 그래서 weight 초기화를 잘못하거나, learning rate를 너무 높게 써서 값이 확 튀면 dead relu가 일어날 수 있다.

0보다 작은 input이 들어와도 gradient를 죽이지 않기 위해 나온 leaky relu이다. 기울기를 learnable parameter로 주는 방식도 있다.
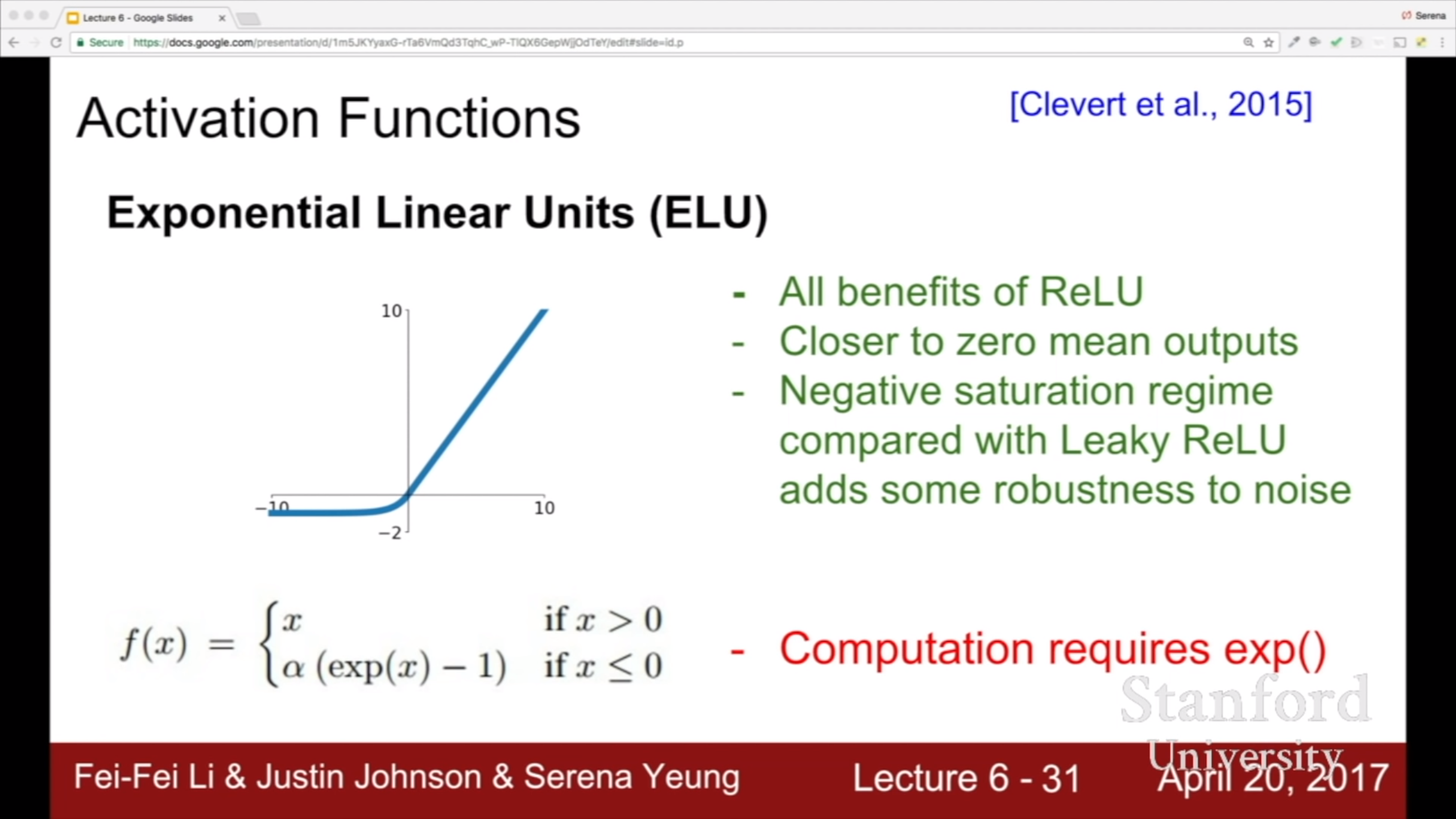
ELU 함수는 relu와 leaky relu를 섞어 놓은 모양이다. Leaky 버전보다 더 robust 하다고 한다.

Maxout이다. Weight를 두 개 만들어서 각각의 output중 큰 값을 반환한다.

얼마 전 리뷰한 ESPCN(yun905.tistory.com/1?category=876803)에서도 relu보다 tanh의 성능이 좋았다고 말했다. 결론은 다 써보는 수 밖에 없다.

데이터 전처리로 넘어와서, zero-centered 되어야 하는 이유는 아까 얘기했던 대로이다. Image의 경우는 std로 나눠주지 않아도 큰 문제는 없는데, 전부 0~255(rgb 기준)라는 어느정도 일정한 scale을 갖기 때문이다. 다른 데이터의 경우 feature마다 scale이 너무 다른 경우도 있어서 이렇게 한다.

이런 복잡한 전처리 방법도 있지만 image를 가지고 낮은 차원에 project 하고 그럴 게 아니라 그냥 그대로 cnn에 넣을 것이기 때문에 사용하지 않을 것이라고 한다. 이 부분에 대해 자세히 설명하지는 않는다.

평균 이미지를 빼거나, per channel mean을 구해서 빼거나 하는데 크게 차이는 없다고 한다. Zero-centered 하게 만들고, 따로 나눠주지는 않아도 잘 된다.

Weight를 모두 같은 값으로 초기화하면 안된다. X와 W는 위와 같이 그릴 수 있는데, 여기서 X1에 대해 각각의 뉴런 W1,W2,W3이 내적을 해서 output을 만든다. 그런데 W1,W2,W3이 모두 같다면, W1과 W2와 W3은 모두 같은 방식으로 업데이트 된다.

그래서 초기화는 random하게 해야 한다. 간단한 weight 초기화 방식으로 어느정도까지는 먹히지만 깊은 네트워크에서는 힘들다. Weight 초기화를 잘못하면 학습이 전혀 일어나지 않을 수도 있다.
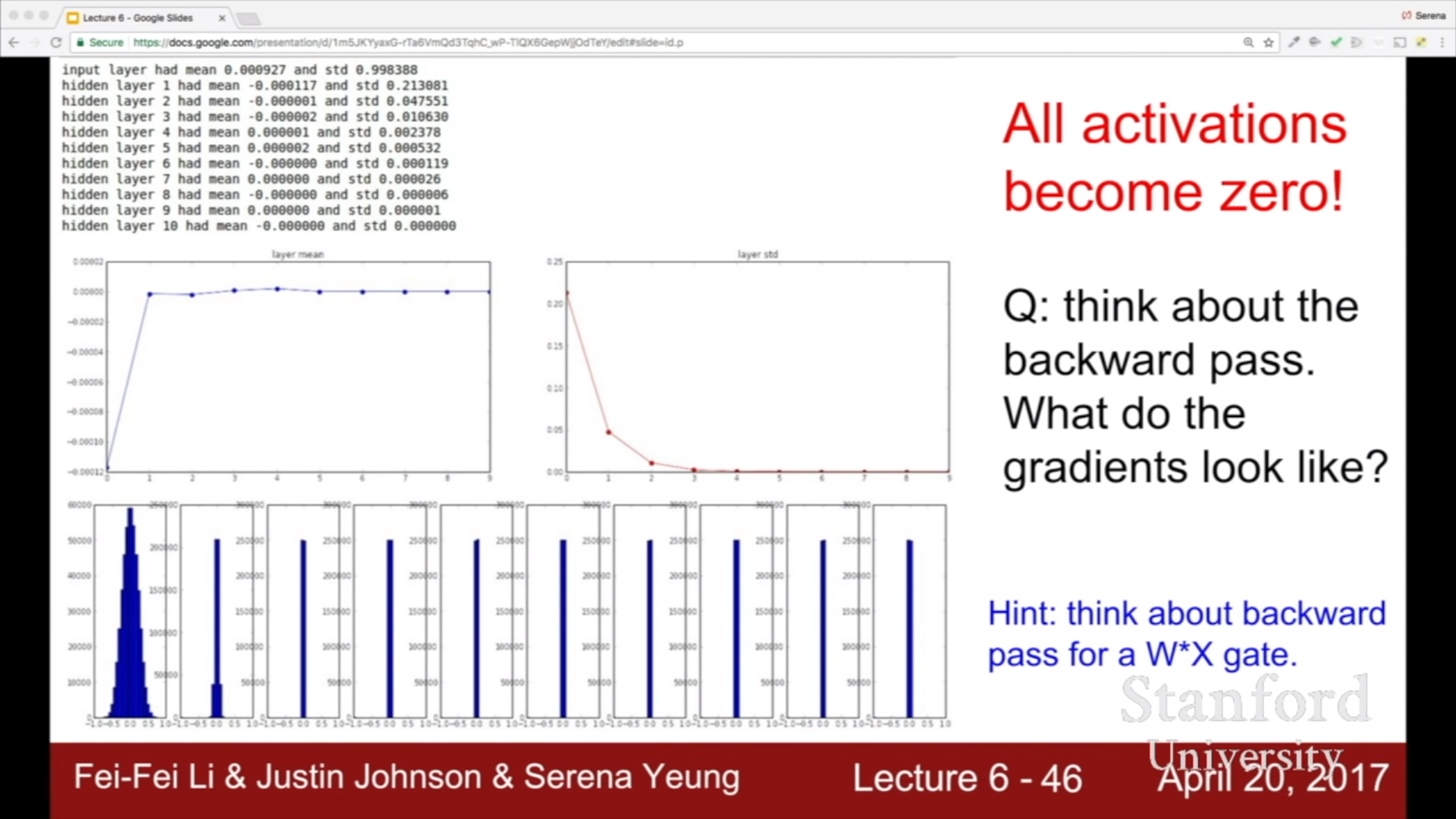
너무 작은 값들을 계속 곱해나가면 output 이 0에 수렴한다. Output은 다음 layer의 input이자 weight의 local gradient가 되는걸 생각해보면 gradient도 0에 수렴할 것이다.

값이 너무 작아서 0에 수렴해서 문제라면 std를 키워볼까? 그러면 이렇게 activation 값이 폭발한다.

거의 default 느낌인 xavier 초기화 방식. Weight의 variance를 1/input_size 로 준다. 뉴럴넷에서 기본적으로 input과 weight를 곱한 후 sum 하기 때문에, input_size가 작으면 그만큼 덧셈이 적게 일어나서 output이 작다. 이것을 보정하기 위해 input_size가 작으면 그에 반비례해서 weight값을 키워주자는 idea이다.

근데 relu는 결과값의 반을 날려버리기 때문에 xavier로는 보정이 잘 안된다.

반을 날려버려서 output이 1/2배 되었으므로, 추가적으로 xavier때의 variance보다 2배 키워준다. 따라서 variance가 2/input_size가 된다.

Weight 초기화를 통해 output의 분포를 조절하는 것은 간접적인 방법이다. 그냥 직접 output을 normalize 하면 되지 않을까? 해서 나온게 batch norm이다. 각 feature 별로 scale이 다를 것이므로 각 feature별 평균과 분산을 구해서 적용한다. CNN의 경우 각 feature map 별로 구한다고 이해했는데, 이후에 assignment에 있다고 하니 그걸 구현하면서 더 깊게 이해해 보겠다.

Output을 가우시안 분포로 만든 후, 그 평균과 분산을 조절할 수 있는 learnable parameter를 붙여서 유연성을 부여한 버전이다. 심지어는 model이 정말로 원한다면 batch norm 이전으로 돌아갈 수도 있다.

장점
-Gradient flow를 좋게 한다. 위에서 봤듯이 output의 분포가 구리면 gradient가 죽는다. Weight 초기화는 간접적으로 그 문제를 해결하려는 방식이고 batch norm은 그 문제를 직접적으로 해결하려는 방식이다.
-Learning rate도 다양하게 쓸 수가 있는데, 값이 폭발해도 batch norm이 scale 해주기 때문인 것 같다. 그래서 model 자체가 다루기 쉬워진다고 한다.
-Weight 초기화가 이루고자 하는 것을 직접적으로 이뤄주기 때문에 거기에 덜 의존하게 된다.
-어떤 input에 대해 batch norm을 한다고 해보면, 거기서 평균을 빼고 표준 편차로 나누고 해야 하는데, 그 평균과 표준 편차는 어디에서 왔을까? 다른 input들과의 연산에서 온 것이다. 즉, 내가 어떤 input인가 뿐만 아니라 나랑 같은 batch에 있는 다른 input은 어떤 애들인가 까지가 고려되어서 내 output이 결정된다는 것이다. 거기서 약간의 random성이 발생하고, 그래서 regularization 효과가 있다.

Model을 babysitting하는 테크닉을 알아볼 것이다. Assignment에서 늘 하던 loss check로 디버깅하는 걸 얘기하고 있다. Regularization strength를 준 후 loss가 올라가는 것 까지 본다.

적은 data로 overfit을 일부러 시켜서 loss가 잘 줄어드는지 확인한다.

Loss는 거의 줄지 않음에도 accuracy가 급격히 좋아지는 이유가 뭘까?
가령 softmax를 지나 얻은 score가 [0.25, 0.25, 0.249, 0.251]이라고 하자. Label은 [0, 0, 0, 1]이라 하자. 그러면 이 모델은 정답을 맞춘 것이다. 하지만 loss를 계산하려고 보면 1과 0.251은 큰 차이가 있다. 그래서 loss는 크게 나올 것이다.
이처럼 accuracy와 loss는 전체적으로 비례하는 모양새이지만 그렇지 않은 지점이 존재한다. 저렇게 accuracy가 급격히 올라간 순간은 아마 score의 마지막 원소가 0.249에서 0.251로 가는 순간과 비슷할 것이다. Loss의 입장에서는 0.002의 차이일 뿐이지만 accuracy의 입장에서는 오답에서 정답으로 바뀐 것이다.

Learning rate이 너무 낮으면 loss가 안떨어지고, 너무 높으면 폭발한다. Hyperparameter를 찾을 때, 처음에는 몇 epoch만 돌려보고 후보를 어느정도 추려서 fine tuning 하는게 좋다.

후보를 추려서 실험을 통해 좋은 learning rate를 찾는 과정이다. 그런데 찾아낸 learning rate가 거의 10^-4에 걸쳐있다. 그러면 10^-5나 10^-6도 실험해볼만 하다.

Grid search보다는 random하게 찾는게 더 좋다. Hyperparameter 중에서도 중요한 게 있고 별로 안 중요한 게 있는데, 왼쪽 그림은 중요한 parameter를 3개밖에 못써봤지만 오른쪽 그림에서 9개를 써볼 수 있었다.

Learning rate의 다양한 모양들.

Loss가 처음에 줄지 않으면 weight 초기화를 잘못 했을 가능성이 있다.